Video: Rasyonel fonksiyonların neden kısıtlamaları vardır?
2024 Yazar: Miles Stephen | [email protected]. Son düzenleme: 2023-12-15 23:41
İhtisas kısıtlamalar bir rasyonel fonksiyon paydayı sıfıra eşitleyerek ve çözerek belirlenebilir. Paydanın sıfıra eşit olduğu x değerleri NS tekillikler denir ve NS etki alanında değil işlev.
Aynı şekilde, rasyonel fonksiyonlar neden önemlidir?
Önem. " Rasyonel fonksiyon "bir kişiye verilen addır işlev polinomların bölümü olarak temsil edilebilir, tıpkı bir akılcı sayı, tam sayıların bir bölümü olarak ifade edilebilen bir sayıdır. rasyonel fonksiyonlar arz önemli örnekler ve birçok bağlamda doğal olarak ortaya çıkar.
Aynı şekilde, rasyonel fonksiyonların dönüm noktaları var mı? 4Özet. n dereceli bir polinom vardır en fazla n gerçek sıfır ve n-1 dönüş noktası . A rasyonel fonksiyon bir işlev f(x)=P(x)Q(x), f (x) = P (x) Q (x) biçimindedir, burada P(x) ve Q(x) NS her iki polinom
Ayrıca soru şu ki, rasyonel bir fonksiyon örneği nedir?
Örnekler ile ilgili Rasyonel Fonksiyonlar NS işlev R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) bir rasyonel fonksiyon pay, x^2 + 4x - 1 bir polinom ve payda, 3x^2 - 9x + 2 de bir polinomdur.
Rasyonel fonksiyonların özellikleri nelerdir?
iki önemli özellikleri herhangi bir rasyonel fonksiyon r(x)=p(x)q(x) r (x) = p (x) q (x) herhangi bir sıfırdır ve düşey asimptotlardır. işlev sahip olabilir. Bu yönleri bir rasyonel fonksiyon sırasıyla pay ve paydanın sıfır olduğu yere yakından bağlıdır.
Önerilen:
Rasyonel ifade için neden kısıtlamalar belirtiriz ve kısıtlamaları ne zaman belirtiriz?
Kısıtlamaları belirtiriz çünkü bu, denklemin bazı x değerlerinde tanımsız olmasına neden olabilir. Rasyonel ifadeler için en yaygın kısıtlama N/0'dır. Bu, sıfıra bölünen herhangi bir sayının tanımsız olduğu anlamına gelir. Örneğin, f(x) = 6/x² işlevi için, x=0'ı değiştirdiğinizde, tanımsız olan 6/0 ile sonuçlanır
AutoCAD'de boyutsal kısıtlamaları nasıl uygularım?
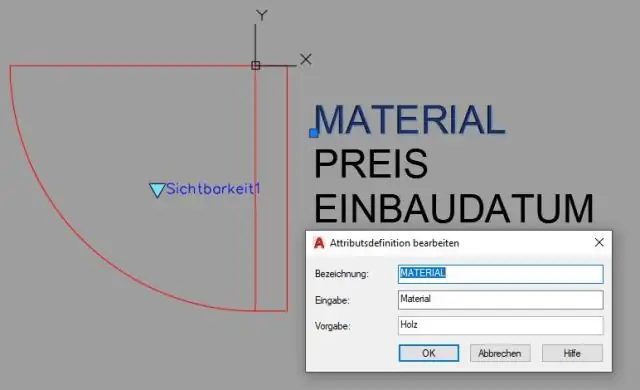
Bu adımlar, boyutsal kısıtlamaların basit bir örneğini sunar: Yeni bir çizim başlatın ve Ribbon's Parametric sekmesini geçerli hale getirin. Durum çubuğunda Snap, Ortho ve Osnap gibi uygun hassas çizim yardımcılarını açın. Hassas bir teknik uygulayarak makul derecede kesin bir geometri çizin
Bir hesap makinesinde logaritmik fonksiyonların grafiğini nasıl çizersiniz?
Grafik hesap makinesinde, temel e logaritması ln tuşudur. Üçü de aynı. logBASE işlevine sahipseniz, işleve girmek için kullanılabilir (aşağıda Y1'de görülmektedir). Değilse, Temel Değişim formülünü kullanın (aşağıdaki Y2'ye bakın)
Tüm lineer fonksiyonların tersi var mı?
Sabit Olmayan Doğrusal Fonksiyonların Tersi. Doğrusal bir fonksiyon, sabit olmadığı veya başka bir deyişle eğimi sıfır olmadığı sürece tersinir olacaktır. Tersini cebirsel olarak veya orijinal doğruyu y = x köşegeni üzerinden yansıtarak grafiksel olarak bulabilirsiniz
Doğrusal fonksiyonların amacı nedir?
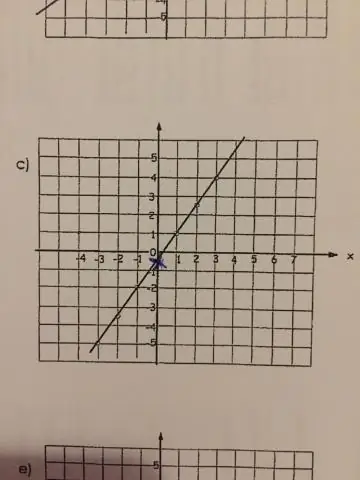
Doğrusal bir fonksiyon, düz bir çizgiye grafik çizen herhangi bir fonksiyondur. Bunun matematiksel olarak anlamı, fonksiyonun üsleri veya güçleri olmayan bir veya iki değişkene sahip olmasıdır. Fonksiyonun daha fazla değişkeni varsa, fonksiyonun doğrusal bir fonksiyon olarak kalması için değişkenlerin sabit veya bilinen değişkenler olması gerekir