Video: Çarpım ve bölüm kuralını nasıl kullanıyorsunuz?
2024 Yazar: Miles Stephen | [email protected]. Son düzenleme: 2023-12-15 23:41
NS Ürün kuralı bir türevi olduğunu söylüyor ürün iki fonksiyonun birinci fonksiyonu çarpı ikinci fonksiyonun türevi artı ikinci fonksiyon çarpı birinci fonksiyonun türevidir. NS Ürün kuralı türevi olduğunda kullanılmalıdır. bölüm alınması gereken iki fonksiyondur.
Bunun yanında çarpım kuralının formülü nedir?
NS Ürün kuralı bir formül türevlerini bulmak için kullanılır. Ürün:% s iki veya daha fazla fonksiyondan (uv)'=u'v+uv'. Δ(uv)=u(x+Δx)v(x+Δx)−u(x)v(x). burada Δu ve Δv sırasıyla u ve v fonksiyonlarının artışlarıdır.
Ayrıca, üsler için çarpım kuralı nedir? Üslü "çarpım kuralı" bize, aynı tabana sahip iki kuvveti çarparken üsleri ekleyebileceğinizi söyler. Bu örnekte, nasıl çalıştığını görebilirsiniz. Üsleri eklemek sadece kısa bir yoldur! NS " güç kuralı "Bize bir gücü bir güce yükseltmenin, sadece çarpmak üsler.
Bu bağlamda, üsler için bölüm kuralı nedir?
Bölüm Kuralı:, bu şunu söylüyor bölmek aynı tabana sahip iki üs, tabanı tutarsınız ve çıkarmak güçler. Bu, kesirleri azaltmaya benzer; sen ne zaman çıkarmak yetkiler, cevabı, daha yüksek gücün bulunduğu yere bağlı olarak pay veya paydaya koyar.
1'in türevi nedir?
NS Türev bize bir fonksiyonun herhangi bir noktadaki eğimini söyler. Birçoğunu bulmak için izleyebileceğimiz kurallar var. türevler . Örneğin: Sabit bir değerin (3 gibi) eğimi her zaman 0'dır.
Türev Tüzük.
| Ortak İşlevler | İşlev | Türev |
|---|---|---|
| Devamlı | C | 0 |
| Hat | x | 1 |
| balta | a | |
| Meydan | x2 | 2 kere |
Önerilen:
68 95 99 kuralını nasıl kullanıyorsunuz?
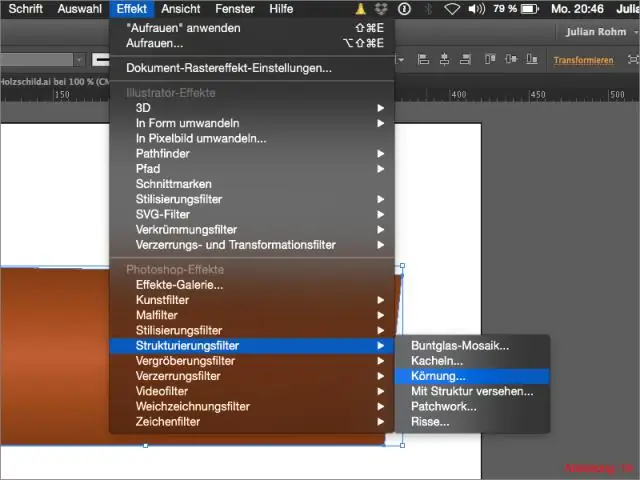
İstatistikte, ampirik kural olarak da bilinen 68-95-99.7 kuralı, iki, dört ve altı standart genişliğinde normal bir dağılımda ortalamanın etrafındaki bir bant içinde yer alan değerlerin yüzdesini hatırlamak için kullanılan bir kestirme yoldur. sırasıyla sapmalar; daha doğrusu, değerlerin %68,27, %95,45 ve %99,73'ü yalan
Çarpım veya bölüm kuralını ne zaman kullanacağınızı nereden biliyorsunuz?
Fonksiyonların bölünmesi. Bu nedenle, iki fonksiyonun çarpımını gördüğünüzde, çarpım kuralını ve bölme durumunda bölüm kuralını kullanın. Fonksiyonun hem çarpması hem de bölümü varsa, her iki kuralı da buna göre kullanın. Genel bir denklem görürseniz, şöyle bir şeydir, tek başına bir fonksiyon nerede
Çapraz çarpım için sağ el kuralını nasıl kullanırsınız?
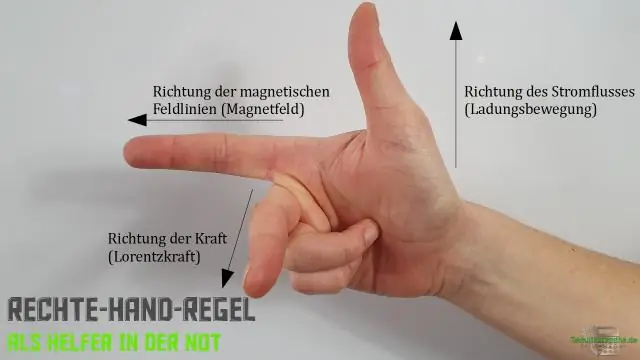
Sağ el kuralı, vektörlerin çapraz çarpımının oryantasyonunun, kuyruktan kuyruğa yerleştirerek, sağ eli düzleştirerek, yönünde uzatarak ve sonra parmakları açının yaptığı yönde kıvırarak belirlendiğini belirtir. Başparmak daha sonra yönü gösterir
Bölüm kuralını ürün kuralına nasıl dönüştürürsünüz?
Bölüm kuralı, ürün ve zincir kurallarının bir uygulaması olarak görülebilir. Eğer Q(x) = f(x)/g(x) ise, o zaman Q(x) = f(x) * 1/(g(x)). Q(x)'in türevini almak için çarpım kuralını kullanabilirsiniz ve 1/(g(x)) u = g(x) ve 1/(g(x)) = 1/u olan zincir kuralı kullanılarak türevlenebilir
Bölüm kuralı yerine çarpım kuralını kullanabilir misiniz?
Bir bölümün türevini almada bölüm kuralının kuvvet kuralı artı çarpım kuralından üstün olmasının iki nedeni vardır: Sonucu basitleştirirken ortak paydaları korur. Kuvvet kuralı artı çarpım kuralını kullanırsanız, sonucu basitleştirmek için genellikle ortak bir payda bulmanız gerekir